🎉 DDPM from scratch

Benjin Zhu

Nov 18, 2024

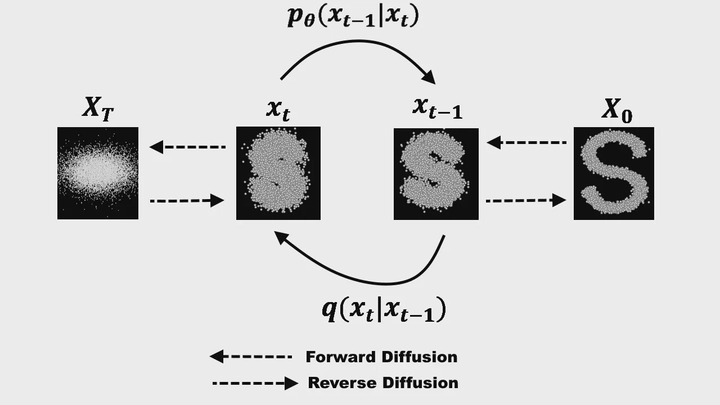Image credit: Unsplash

pip install -q diffusers

Note: you may need to restart the kernel to use updated packages.

import torch
import torchvision
from torch import nn
from torch.nn import functional as F
from torch.utils.data import DataLoader

from diffusers import DDPMScheduler, UNet2DModel
from matplotlib import pyplot as plt

device = torch.device("cuda:1")

dataset = torchvision.datasets.FashionMNIST(
    root="fashio_mnist/", train=True, download=True, transform=torchvision.transforms.ToTensor()
)

Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-images-idx3-ubyte.gz
Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-images-idx3-ubyte.gz to fashio_mnist/FashionMNIST/raw/train-images-idx3-ubyte.gz


100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 26.4M/26.4M [00:02<00:00, 9.16MB/s]


Extracting fashio_mnist/FashionMNIST/raw/train-images-idx3-ubyte.gz to fashio_mnist/FashionMNIST/raw

Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-labels-idx1-ubyte.gz
Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/train-labels-idx1-ubyte.gz to fashio_mnist/FashionMNIST/raw/train-labels-idx1-ubyte.gz


100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 29.5k/29.5k [00:00<00:00, 153kB/s]


Extracting fashio_mnist/FashionMNIST/raw/train-labels-idx1-ubyte.gz to fashio_mnist/FashionMNIST/raw

Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-images-idx3-ubyte.gz
Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-images-idx3-ubyte.gz to fashio_mnist/FashionMNIST/raw/t10k-images-idx3-ubyte.gz


100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 4.42M/4.42M [00:01<00:00, 2.78MB/s]


Extracting fashio_mnist/FashionMNIST/raw/t10k-images-idx3-ubyte.gz to fashio_mnist/FashionMNIST/raw

Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-labels-idx1-ubyte.gz
Downloading http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/t10k-labels-idx1-ubyte.gz to fashio_mnist/FashionMNIST/raw/t10k-labels-idx1-ubyte.gz


100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 5.15k/5.15k [00:00<00:00, 8.46MB/s]

Extracting fashio_mnist/FashionMNIST/raw/t10k-labels-idx1-ubyte.gz to fashio_mnist/FashionMNIST/raw

train_dataloader = DataLoader(dataset, batch_size=8, shuffle=True)

x, y = next(iter(train_dataloader))
print("Input shape:", x.shape)
print("Labels:", y)
plt.imshow(torchvision.utils.make_grid(x)[0], cmap="Greys")

Input shape: torch.Size([8, 1, 28, 28])
Labels: tensor([3, 7, 5, 1, 4, 0, 7, 6])





<matplotlib.image.AxesImage at 0x7fbb20240f80>

def corrupt(x, amount):
    noise = torch.rand_like(x)
    amount = amount.view(-1, 1, 1, 1)
    return x * (1-amount) + noise * amount

fig, axs = plt.subplots(2, 1, figsize=(12, 5))
axs[0].set_title("Input data")
axs[0].imshow(torchvision.utils.make_grid(x)[0], cmap="Greys")

amount = torch.linspace(0, 1, x.shape[0])
noised_x = corrupt(x, amount)

axs[1].set_title("Corrupted data --> increase")
axs[1].imshow(torchvision.utils.make_grid(noised_x)[0], cmap="Greys")

<matplotlib.image.AxesImage at 0x7fbb2024df40>

print(help(torch.rand_like))

Help on built-in function rand_like in module torch:

rand_like(...)
    rand_like(input, *, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format) -> Tensor

    Returns a tensor with the same size as :attr:`input` that is filled with
    random numbers from a uniform distribution on the interval :math:`[0, 1)`.
    ``torch.rand_like(input)`` is equivalent to
    ``torch.rand(input.size(), dtype=input.dtype, layout=input.layout, device=input.device)``.

    Args:
        input (Tensor): the size of :attr:`input` will determine size of the output tensor.

    Keyword args:
        dtype (:class:`torch.dtype`, optional): the desired data type of returned Tensor.
            Default: if ``None``, defaults to the dtype of :attr:`input`.
        layout (:class:`torch.layout`, optional): the desired layout of returned tensor.
            Default: if ``None``, defaults to the layout of :attr:`input`.
        device (:class:`torch.device`, optional): the desired device of returned tensor.
            Default: if ``None``, defaults to the device of :attr:`input`.
        requires_grad (bool, optional): If autograd should record operations on the
            returned tensor. Default: ``False``.
        memory_format (:class:`torch.memory_format`, optional): the desired memory format of
            returned Tensor. Default: ``torch.preserve_format``.

None

class BasicUNet(nn.Module):
    def __init__(self, in_channels=1, out_channels=1):
        super().__init__()
        self.down_layers = torch.nn.ModuleList(
            [
                nn.Conv2d(in_channels, 32, kernel_size=5, padding=2),
                nn.Conv2d(32, 64, kernel_size=5, padding=2),
                nn.Conv2d(64, 64, kernel_size=5, padding=2),
            ]
        )
        self.up_layers = torch.nn.ModuleList(
            [
                nn.Conv2d(64, 64, kernel_size=5, padding=2),
                nn.Conv2d(64, 32, kernel_size=5, padding=2),
                nn.Conv2d(32, out_channels, kernel_size=5, padding=2),
            ]
        )

        self.act = nn.SiLU()
        self.downscale = nn.MaxPool2d(2)
        self.upscale = nn.Upsample(scale_factor=2)

    def forward(self, x):
        h = []
        for i, l in enumerate(self.down_layers):
            x = self.act(l(x))
            if i < 2:
                h.append(x)
                x = self.downscale(x)

        for i, l in enumerate(self.up_layers):
            if i > 0:
                x = self.upscale(x)
                x += h.pop()
            x = self.act(l(x))

        return x

net = BasicUNet()
x = torch.rand(8, 1, 28, 28)
net(x).shape

torch.Size([8, 1, 28, 28])

sum([p.numel() for p in net.parameters()])

print(help(torch.numel))

Help on built-in function numel in module torch:

numel(...)
    numel(input) -> int

    Returns the total number of elements in the :attr:`input` tensor.

    Args:
        input (Tensor): the input tensor.

    Example::

        >>> a = torch.randn(1, 2, 3, 4, 5)
        >>> torch.numel(a)
        120
        >>> a = torch.zeros(4,4)
        >>> torch.numel(a)
        16

None

# Dataloader (you can mess with batch size)
batch_size = 128
train_dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

# How many runs through the data should we do?
n_epochs = 10

# Create the network
net = BasicUNet()
net.to(device)

# Our loss function
loss_fn = nn.MSELoss()

# The optimizer
opt = torch.optim.Adam(net.parameters(), lr=1e-3)

# Keeping a record of the losses for later viewing
losses = []

# The training loop
for epoch in range(n_epochs):

    for x, y in train_dataloader:

        # Get some data and prepare the corrupted version
        x = x.to(device)  # Data on the GPU
        noise_amount = torch.rand(x.shape[0]).to(device)  # Pick random noise amounts
        noisy_x = corrupt(x, noise_amount)  # Create our noisy x

        # Get the model prediction
        pred = net(noisy_x)

        # Calculate the loss
        loss = loss_fn(pred, x)  # How close is the output to the true 'clean' x?

        # Backprop and update the params:
        opt.zero_grad()
        loss.backward()
        opt.step()

        # Store the loss for later
        losses.append(loss.item())

    # Print our the average of the loss values for this epoch:
    avg_loss = sum(losses[-len(train_dataloader) :]) / len(train_dataloader)
    print(f"Finished epoch {epoch}. Average loss for this epoch: {avg_loss:05f}")

# View the loss curve
plt.plot(losses)
plt.ylim(0, 0.1)

Finished epoch 0. Average loss for this epoch: 0.033161
Finished epoch 1. Average loss for this epoch: 0.024507
Finished epoch 2. Average loss for this epoch: 0.022048
Finished epoch 3. Average loss for this epoch: 0.020974
Finished epoch 4. Average loss for this epoch: 0.020429
Finished epoch 5. Average loss for this epoch: 0.019486
Finished epoch 6. Average loss for this epoch: 0.019203
Finished epoch 7. Average loss for this epoch: 0.018884
Finished epoch 8. Average loss for this epoch: 0.018868
Finished epoch 9. Average loss for this epoch: 0.018572





(0.0, 0.1)

# @markdown Visualizing model predictions on noisy inputs:

# Fetch some data
x, y = next(iter(train_dataloader))
x = x[:8]  # Only using the first 8 for easy plotting

# Corrupt with a range of amounts
amount = torch.linspace(0, 1, x.shape[0])  # Left to right -> more corruption
noised_x = corrupt(x, amount)

# Get the model predictions
preds = noised_x.to(device)
with torch.no_grad():
    for i in range(5):
        preds = net(preds)
        if i == 0:
            first_preds = preds.detach().cpu()
    preds = preds.detach().cpu()

# Plot
fig, axs = plt.subplots(4, 1, figsize=(12, 7))
axs[0].set_title("Input data")
axs[0].imshow(torchvision.utils.make_grid(x)[0].clip(0, 1), cmap="Greys")
axs[1].set_title("Corrupted data")
axs[1].imshow(torchvision.utils.make_grid(noised_x)[0].clip(0, 1), cmap="Greys")
axs[2].set_title("Network Predictions (1 pass)")
axs[2].imshow(torchvision.utils.make_grid(first_preds)[0].clip(0, 1), cmap="Greys")
axs[3].set_title("Network Predictions (5 passes)")
axs[3].imshow(torchvision.utils.make_grid(preds)[0].clip(0, 1), cmap="Greys")

<matplotlib.image.AxesImage at 0x7fbbc96163f0>

Sampling

# @markdown Sampling strategy: Break the process into 5 steps and move 1/5'th of the way there each time:
n_steps = 5
x = torch.rand(8, 1, 28, 28).to(device)  # Start from random
step_history = [x.detach().cpu()]
pred_output_history = []

for i in range(n_steps):
    with torch.no_grad():  # No need to track gradients during inference
        pred = net(x)  # Predict the denoised x0
    pred_output_history.append(pred.detach().cpu())  # Store model output for plotting
    mix_factor = 1 / (n_steps - i)  # How much we move towards the prediction
    x = x * (1 - mix_factor) + pred * mix_factor  # Move part of the way there
    step_history.append(x.detach().cpu())  # Store step for plotting

fig, axs = plt.subplots(n_steps, 2, figsize=(9, 4), sharex=True)
axs[0, 0].set_title("x (model input)")
axs[0, 1].set_title("model prediction")
for i in range(n_steps):
    axs[i, 0].imshow(torchvision.utils.make_grid(step_history[i])[0].clip(0, 1), cmap="Greys")
    axs[i, 1].imshow(torchvision.utils.make_grid(pred_output_history[i])[0].clip(0, 1), cmap="Greys")

# @markdown Showing more results, using 40 sampling steps
n_steps = 40
x = torch.rand(64, 1, 28, 28).to(device)
for i in range(n_steps):
    noise_amount = torch.ones((x.shape[0],)).to(device) * (1 - (i / n_steps))  # Starting high going low
    with torch.no_grad():
        pred = net(x)
    mix_factor = 1 / (n_steps - i)
    x = x * (1 - mix_factor) + pred * mix_factor
fig, ax = plt.subplots(1, 1, figsize=(12, 12))
ax.imshow(torchvision.utils.make_grid(x.detach().cpu(), nrow=8)[0].clip(0, 1), cmap="Greys")

<matplotlib.image.AxesImage at 0x7fbb181283e0>

model = UNet2DModel(
    sample_size=28,  # the target image resolution
    in_channels=1,  # the number of input channels, 3 for RGB images
    out_channels=1,  # the number of output channels
    layers_per_block=2,  # how many ResNet layers to use per UNet block
    block_out_channels=(32, 64, 64),  # Roughly matching our basic unet example
    down_block_types=(
        "DownBlock2D",  # a regular ResNet downsampling block
        "AttnDownBlock2D",  # a ResNet downsampling block with spatial self-attention
        "AttnDownBlock2D",
    ),
    up_block_types=(
        "AttnUpBlock2D",
        "AttnUpBlock2D",  # a ResNet upsampling block with spatial self-attention
        "UpBlock2D",  # a regular ResNet upsampling block
    ),
)
print(model)

UNet2DModel(
  (conv_in): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (time_proj): Timesteps()
  (time_embedding): TimestepEmbedding(
    (linear_1): Linear(in_features=32, out_features=128, bias=True)
    (act): SiLU()
    (linear_2): Linear(in_features=128, out_features=128, bias=True)
  )
  (down_blocks): ModuleList(
    (0): DownBlock2D(
      (resnets): ModuleList(
        (0-1): 2 x ResnetBlock2D(
          (norm1): GroupNorm(32, 32, eps=1e-05, affine=True)
          (conv1): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=32, bias=True)
          (norm2): GroupNorm(32, 32, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
        )
      )
      (downsamplers): ModuleList(
        (0): Downsample2D(
          (conv): Conv2d(32, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
        )
      )
    )
    (1): AttnDownBlock2D(
      (attentions): ModuleList(
        (0-1): 2 x Attention(
          (group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
          (to_q): Linear(in_features=64, out_features=64, bias=True)
          (to_k): Linear(in_features=64, out_features=64, bias=True)
          (to_v): Linear(in_features=64, out_features=64, bias=True)
          (to_out): ModuleList(
            (0): Linear(in_features=64, out_features=64, bias=True)
            (1): Dropout(p=0.0, inplace=False)
          )
        )
      )
      (resnets): ModuleList(
        (0): ResnetBlock2D(
          (norm1): GroupNorm(32, 32, eps=1e-05, affine=True)
          (conv1): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
          (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
          (conv_shortcut): Conv2d(32, 64, kernel_size=(1, 1), stride=(1, 1))
        )
        (1): ResnetBlock2D(
          (norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
          (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
          (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
        )
      )
      (downsamplers): ModuleList(
        (0): Downsample2D(
          (conv): Conv2d(64, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
        )
      )
    )
    (2): AttnDownBlock2D(
      (attentions): ModuleList(
        (0-1): 2 x Attention(
          (group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
          (to_q): Linear(in_features=64, out_features=64, bias=True)
          (to_k): Linear(in_features=64, out_features=64, bias=True)
          (to_v): Linear(in_features=64, out_features=64, bias=True)
          (to_out): ModuleList(
            (0): Linear(in_features=64, out_features=64, bias=True)
            (1): Dropout(p=0.0, inplace=False)
          )
        )
      )
      (resnets): ModuleList(
        (0-1): 2 x ResnetBlock2D(
          (norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
          (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
          (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
        )
      )
    )
  )
  (up_blocks): ModuleList(
    (0): AttnUpBlock2D(
      (attentions): ModuleList(
        (0-2): 3 x Attention(
          (group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
          (to_q): Linear(in_features=64, out_features=64, bias=True)
          (to_k): Linear(in_features=64, out_features=64, bias=True)
          (to_v): Linear(in_features=64, out_features=64, bias=True)
          (to_out): ModuleList(
            (0): Linear(in_features=64, out_features=64, bias=True)
            (1): Dropout(p=0.0, inplace=False)
          )
        )
      )
      (resnets): ModuleList(
        (0-2): 3 x ResnetBlock2D(
          (norm1): GroupNorm(32, 128, eps=1e-05, affine=True)
          (conv1): Conv2d(128, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
          (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
          (conv_shortcut): Conv2d(128, 64, kernel_size=(1, 1), stride=(1, 1))
        )
      )
      (upsamplers): ModuleList(
        (0): Upsample2D(
          (conv): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
        )
      )
    )
    (1): AttnUpBlock2D(
      (attentions): ModuleList(
        (0-2): 3 x Attention(
          (group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
          (to_q): Linear(in_features=64, out_features=64, bias=True)
          (to_k): Linear(in_features=64, out_features=64, bias=True)
          (to_v): Linear(in_features=64, out_features=64, bias=True)
          (to_out): ModuleList(
            (0): Linear(in_features=64, out_features=64, bias=True)
            (1): Dropout(p=0.0, inplace=False)
          )
        )
      )
      (resnets): ModuleList(
        (0-1): 2 x ResnetBlock2D(
          (norm1): GroupNorm(32, 128, eps=1e-05, affine=True)
          (conv1): Conv2d(128, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
          (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
          (conv_shortcut): Conv2d(128, 64, kernel_size=(1, 1), stride=(1, 1))
        )
        (2): ResnetBlock2D(
          (norm1): GroupNorm(32, 96, eps=1e-05, affine=True)
          (conv1): Conv2d(96, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
          (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
          (conv_shortcut): Conv2d(96, 64, kernel_size=(1, 1), stride=(1, 1))
        )
      )
      (upsamplers): ModuleList(
        (0): Upsample2D(
          (conv): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
        )
      )
    )
    (2): UpBlock2D(
      (resnets): ModuleList(
        (0): ResnetBlock2D(
          (norm1): GroupNorm(32, 96, eps=1e-05, affine=True)
          (conv1): Conv2d(96, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=32, bias=True)
          (norm2): GroupNorm(32, 32, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
          (conv_shortcut): Conv2d(96, 32, kernel_size=(1, 1), stride=(1, 1))
        )
        (1-2): 2 x ResnetBlock2D(
          (norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
          (conv1): Conv2d(64, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (time_emb_proj): Linear(in_features=128, out_features=32, bias=True)
          (norm2): GroupNorm(32, 32, eps=1e-05, affine=True)
          (dropout): Dropout(p=0.0, inplace=False)
          (conv2): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
          (nonlinearity): SiLU()
          (conv_shortcut): Conv2d(64, 32, kernel_size=(1, 1), stride=(1, 1))
        )
      )
    )
  )
  (mid_block): UNetMidBlock2D(
    (attentions): ModuleList(
      (0): Attention(
        (group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
        (to_q): Linear(in_features=64, out_features=64, bias=True)
        (to_k): Linear(in_features=64, out_features=64, bias=True)
        (to_v): Linear(in_features=64, out_features=64, bias=True)
        (to_out): ModuleList(
          (0): Linear(in_features=64, out_features=64, bias=True)
          (1): Dropout(p=0.0, inplace=False)
        )
      )
    )
    (resnets): ModuleList(
      (0-1): 2 x ResnetBlock2D(
        (norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
        (time_emb_proj): Linear(in_features=128, out_features=64, bias=True)
        (norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
        (dropout): Dropout(p=0.0, inplace=False)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
        (nonlinearity): SiLU()
      )
    )
  )
  (conv_norm_out): GroupNorm(32, 32, eps=1e-05, affine=True)
  (conv_act): SiLU()
  (conv_out): Conv2d(32, 1, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
)

sum([p.numel() for p in model.parameters()])  # 1.7M vs the ~309k parameters of the BasicUNet

# @markdown Trying UNet2DModel instead of BasicUNet:

# Dataloader (you can mess with batch size)
batch_size = 128
train_dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

# How many runs through the data should we do?
n_epochs = 10

# Create the network
net = UNet2DModel(
    sample_size=28,  # the target image resolution
    in_channels=1,  # the number of input channels, 3 for RGB images
    out_channels=1,  # the number of output channels
    layers_per_block=2,  # how many ResNet layers to use per UNet block
    block_out_channels=(32, 64, 64),  # Roughly matching our basic unet example
    down_block_types=(
        "DownBlock2D",  # a regular ResNet downsampling block
        "AttnDownBlock2D",  # a ResNet downsampling block with spatial self-attention
        "AttnDownBlock2D",
    ),
    up_block_types=(
        "AttnUpBlock2D",
        "AttnUpBlock2D",  # a ResNet upsampling block with spatial self-attention
        "UpBlock2D",  # a regular ResNet upsampling block
    ),
)  # <<<
net.to(device)

# Our loss finction
loss_fn = nn.MSELoss()

# The optimizer
opt = torch.optim.Adam(net.parameters(), lr=1e-3)

# Keeping a record of the losses for later viewing
losses = []

# The training loop
for epoch in range(n_epochs):

    for x, y in train_dataloader:

        # Get some data and prepare the corrupted version
        x = x.to(device)  # Data on the GPU
        noise_amount = torch.rand(x.shape[0]).to(device)  # Pick random noise amounts
        noisy_x = corrupt(x, noise_amount)  # Create our noisy x

        # Get the model prediction
        pred = net(noisy_x, 0).sample  # <<< Using timestep 0 always, adding .sample

        # Calculate the loss
        loss = loss_fn(pred, x)  # How close is the output to the true 'clean' x?

        # Backprop and update the params:
        opt.zero_grad()
        loss.backward()
        opt.step()

        # Store the loss for later
        losses.append(loss.item())

    # Print our the average of the loss values for this epoch:
    avg_loss = sum(losses[-len(train_dataloader) :]) / len(train_dataloader)
    print(f"Finished epoch {epoch}. Average loss for this epoch: {avg_loss:05f}")

# Plot losses and some samples
fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# Losses
axs[0].plot(losses)
axs[0].set_ylim(0, 0.1)
axs[0].set_title("Loss over time")

# Samples
n_steps = 40
x = torch.rand(64, 1, 28, 28).to(device)
for i in range(n_steps):
    noise_amount = torch.ones((x.shape[0],)).to(device) * (1 - (i / n_steps))  # Starting high going low
    with torch.no_grad():
        pred = net(x, 0).sample
    mix_factor = 1 / (n_steps - i)
    x = x * (1 - mix_factor) + pred * mix_factor

axs[1].imshow(torchvision.utils.make_grid(x.detach().cpu(), nrow=8)[0].clip(0, 1), cmap="Greys")
axs[1].set_title("Generated Samples")

Finished epoch 0. Average loss for this epoch: 0.027586
Finished epoch 1. Average loss for this epoch: 0.017064
Finished epoch 2. Average loss for this epoch: 0.015153
Finished epoch 3. Average loss for this epoch: 0.013914
Finished epoch 4. Average loss for this epoch: 0.013648
Finished epoch 5. Average loss for this epoch: 0.012831
Finished epoch 6. Average loss for this epoch: 0.012541
Finished epoch 7. Average loss for this epoch: 0.012179
Finished epoch 8. Average loss for this epoch: 0.011927
Finished epoch 9. Average loss for this epoch: 0.011639





Text(0.5, 1.0, 'Generated Samples')

noise_scheduler = DDPMScheduler(num_train_timesteps=1000)
plt.plot(noise_scheduler.alphas_cumprod.cpu() ** 0.5, label=r"${\sqrt{\bar{\alpha}_t}}$")
plt.plot((1 - noise_scheduler.alphas_cumprod.cpu()) ** 0.5, label=r"$\sqrt{(1 - \bar{\alpha}_t)}$")
plt.legend(fontsize="x-large")

<matplotlib.legend.Legend at 0x7fbbc9b32ed0>

# @markdown visualize the DDPM noising process for different timesteps:

# Noise a batch of images to view the effect
fig, axs = plt.subplots(3, 1, figsize=(16, 10))
xb, yb = next(iter(train_dataloader))
xb = xb.to(device)[:8]
xb = xb * 2.0 - 1.0  # Map to (-1, 1)
print("X shape", xb.shape)

# Show clean inputs
axs[0].imshow(torchvision.utils.make_grid(xb[:8])[0].detach().cpu(), cmap="Greys")
axs[0].set_title("Clean X")

# Add noise with scheduler
timesteps = torch.linspace(0, 999, 8).long().to(device)
noise = torch.randn_like(xb)  # << NB: randn not rand
noisy_xb = noise_scheduler.add_noise(xb, noise, timesteps)
print("Noisy X shape", noisy_xb.shape)

# Show noisy version (with and without clipping)
axs[1].imshow(torchvision.utils.make_grid(noisy_xb[:8])[0].detach().cpu().clip(-1, 1), cmap="Greys")
axs[1].set_title("Noisy X (clipped to (-1, 1)")
axs[2].imshow(torchvision.utils.make_grid(noisy_xb[:8])[0].detach().cpu(), cmap="Greys")
axs[2].set_title("Noisy X")

X shape torch.Size([8, 1, 28, 28])
Noisy X shape torch.Size([8, 1, 28, 28])





Text(0.5, 1.0, 'Noisy X')

noise = torch.randn_like(xb)  # Random Gaussian noise
noisy_x = noise_scheduler.add_noise(xb, noise, timesteps)  # Add noise
model_prediction = model(noisy_x, timesteps).sample  # Predict the noise
loss = mse_loss(model_prediction, noise)  # Compute the loss with actual noise

---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

Cell In[73], line 4
      2 noisy_x = noise_scheduler.add_noise(xb, noise, timesteps)  # Add noise
      3 model_prediction = model(noisy_x, timesteps).sample  # Predict the noise
----> 4 loss = mse_loss(model_prediction, noise)  # Compute the loss with actual noise


NameError: name 'mse_loss' is not defined

The corruption process in the context of Denoising Diffusion Probabilistic Models (DDPM) is a method for progressively adding noise to data over multiple steps, simulating a diffusion process. Let’s break it down:

Key Concepts in the Corruption Process

1.	Corruption by Noise Addition:
•	At each timestep , noise is added to the data  to create .
•	This process follows the equation:

Here: • : Scales down the signal from the previous timestep. • : Determines the magnitude of the added noise. • : Represents a Gaussian distribution, ensuring that the noise follows a normal distribution. • Interpretation: This step scales down the original input slightly and mixes it with Gaussian noise. The parameter (set by a predefined schedule) determines how much noise is added at each timestep.

2.	Cumulative Noise Across Timesteps:
•	Instead of applying the noise step-by-step (e.g., 500 iterations to reach ), the process can directly compute  at any timestep  given the original data :

Here: • , where . • : Determines how much of the original input remains after steps. • : Determines how much noise has accumulated. • Interpretation: The process is a linear combination of the original input and Gaussian noise, where the contributions shift from mostly to mostly noise over time.

3.	Scheduler for Noise Addition:
•	A scheduler (like DDPMScheduler) automates this process by defining the  schedule and computing .
•	Visualization of  and :
•	 starts near 1, meaning the data remains mostly intact.
•	Over time,  decreases and  increases, showing that noise dominates.

Visualizing the Corruption Process

•	In practice, we can visualize how the data becomes noisier over time:
•	Clean Input: Starts with the original data (e.g., an image).
•	Progressive Noising: Noise is added at each timestep using Gaussian noise  (from torch.randn).
•	Scheduler Handling: A noise scheduler (DDPMScheduler) ensures that the noise is applied correctly according to the schedule.

Gaussian vs. Uniform Noise

•	Unlike uniform noise (random values between 0 and 1), Gaussian noise is centered around 0 with a standard deviation of 1. This provides smoother corruption and better aligns with the Gaussian assumptions in the model.

Normalization

•	Why Normalize: The training data is often normalized to ensure the model learns efficiently. A common normalization maps data from  to , aligning with the range of the noise.
•	Effect on Data: Ensures that the data and noise scales match, preventing one from dominating the learning process.

Summary

The corruption process in DDPM: 1. Gradually adds noise to data in multiple steps, controlled by a schedule (). 2. Allows direct computation of any timestep’s noisy version given the original input . 3. Uses Gaussian noise for smooth corruption, and normalization ensures the data and noise are on compatible scales.

This process is crucial for training DDPMs, as the model learns to reverse this noising process and generate data by denoising.

Training Objectives

1.	Noise Prediction: The model predicts the noise added during corruption. This simplifies training and provides favorable loss weighting.
2.	Loss Weighting: Implicitly emphasizes low noise levels, improving denoising performance.
3.	Alternative Objectives: Predicting denoised images, velocities, or using scaled losses may improve results in specific tasks.
4.	Ongoing Research: Future objectives will likely refine or replace noise prediction as new insights emerge.

By choosing the right training objective, we can significantly influence the model’s performance and efficiency in diffusion-based generative modeling.

Weighting Effect from the Noise Scale

At each timestep t , the input \mathbf{x}_t is:

\mathbf{x}_t = \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon

Where: • \sqrt{\bar{\alpha}_t} : Scales the contribution of the original image. • \sqrt{1 - \bar{\alpha}_t} : Scales the contribution of the noise.

For High Noise Levels (High t ):

•	 \sqrt{1 - \bar{\alpha}_t}  dominates.
•	 \mathbf{x}_t  is mostly noise, making it harder for the model to learn meaningful information.
•	The MSE loss value is generally higher, but the gradients for improving the model are less informative because the task is harder.

For Low Noise Levels (Low t ):

•	 \sqrt{\bar{\alpha}_t}  dominates.
•	 \mathbf{x}_t  retains more of the original image, making it easier for the model to accurately predict the noise.
•	The MSE loss is smaller, but the model learns more effectively from these “easier” cases.

Key Points on Diffusion Models

1. Corruption Process

Noise Addition:
- Data is progressively corrupted by adding Gaussian noise over multiple timesteps.
- At each timestep ( t ), noise is added based on:
```
q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I})
```
Direct Computation:
- Noise at any timestep ( t ) can be computed directly from the original data ( \mathbf{x}_0 ) as:
```
q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, \sqrt{1 - \bar{\alpha}_t} \mathbf{I})
```
  where ( \bar{\alpha}t = \prod{i=1}^t (1 - \beta_i) ).

2. Training Objective

Noise Prediction:
- The model learns to predict the noise added to the data during the corruption process rather than directly predicting the denoised image.
- The loss is computed as:
```
\text{loss} = \text{MSE}(\epsilon_\text{pred}, \epsilon)
```
- Predicting noise simplifies training due to the linear relationship between ( \mathbf{x}_t ), ( \mathbf{x}_0 ), and noise ( \epsilon ).
Implicit Loss Weighting:
- Predicting noise places greater emphasis on low noise levels (early timesteps), which aligns with the denoising task’s final steps and improves quality.
Alternative Objectives:
- Predicting the denoised image, velocity, or using scaled losses can provide different trade-offs in model performance and sampling quality.

3. Sampling

Iterative Denoising:

Sampling starts with pure noise and iteratively removes noise in multiple timesteps based on the model’s predictions.

At each step:

\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(\mathbf{x}_t, t) \right) + \sigma_t z

Key Design Questions:
- Step size: Smaller steps improve quality but increase computational cost.
- Prediction method: Use single-step (e.g., DDPM) or higher-order methods (e.g., ODE solvers).
- Stochasticity: Adding randomness can improve diversity, while deterministic sampling ensures reproducibility.
Trade-Offs:
- High-quality results require more steps, but research (e.g., DDIM) focuses on reducing steps while maintaining quality.

4. Timestep Conditioning

The model takes both the noisy input ( \mathbf{x}_t ) and the timestep ( t ) as inputs.
Timestep information helps the model adapt its predictions based on the noise level, improving performance.

5. Popularization and Advancements

“Denoising Diffusion Probabilistic Models” (DDPM) by Ho et al. (2020):
- Popularized diffusion models and demonstrated their potential in image synthesis.
Extensions and Improvements:
- DDIM: Deterministic sampling with fewer steps.
- Progressive Distillation: Faster sampling with fewer steps.
- Latent Diffusion Models (LDMs): Perform diffusion in latent space for computational efficiency.